Topological defects

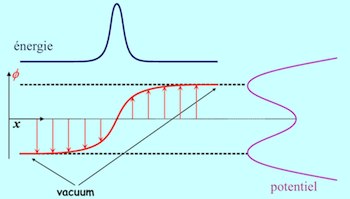
Topological defects are a generic consequence of phase transitions if a field has a topologically non-trivial vacuum. They are common in condensed matter physics, for example in liquid crystals or in protein folding. Other well-known examples are flux-tubes in superconductors or vortices in superfluid helium. The simplest example of a topological defect occurs in 1+1 dimensions for a field with a Mexican hat type potential of the form V(φ) ~ (φ²-v²)², see first drawing. The vacuum (or lowest energy states) are at φ=±v. If, as shown in the figure, the field is in the lower vacuum on the left, and in the upper vacuum on the right, then it will need to move across the central 'hump' in the potential somewhere in between, this is the defect. Near the defect, the energy is higher due to the field gradient and the contribution from the potential. The defect itself cannot disappear spontaneously, it can only move along the x-axis.

Phase transitions are thought to occur in the early universe, for example at the end of inflation. If topological defects are generated in such a phase transition, then they will create additional perturbations that may be detectable for example in the Cosmic Microwave Background. In order to make predictions, we have to resort to numerical simulations of the defects. An example of a cosmic string simulation by David Daverio is shown in the second picture. Cosmic strings are line-like topological defects, a slightly more technical introduction to cosmic strings and their cosmological importance was given by Mark Hindmarsh [arXiv:1106.0391].

You can also read about our research in an article by Simone Ulmer for the CSCS.